Unidad 3: Tipos de discontinuidad

Tipos de discontinuidad

Discontinuidad evitable

Si una función tiene límite en un punto, pero la función en ese punto tiene un valor distinto:

o no existe:

se dice que la discontinuidad es evitable, asignando a la función, en ese punto, el valor del límite:

Discontinuidad esencial o no evitable

Se dice que una función presenta una discontinuidad esencial cuando se produce algunas de las siguientes situaciones:

Discontinuidad de primera especie: si los límites laterales son distintos, o al menos uno de ellos diverge.

Discontinuidad de segunda especie: si la función, al menos en uno de los lados del punto, no existe o no tiene límite.

Discontinuidad de primera especie

En este tipo de discontinuidad existen tres tipos:

De salto finito

Existen el límite por la derecha y por la izquierda del punto, su valor es finito, pero no son iguales:

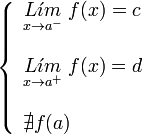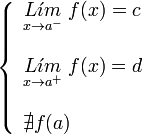A este tipo de discontinuidad de primera especie se le llama salto finito, y el salto viene dado por:Si la función tiende a c, cuando x tiende a a por la izquierda, y tiende a d cuando lo hace por la derecha, en el punto x = a, se presenta un salto, independientemente del valor de la función en ese punto.

Así podemos ver que son discontinuidades de salto finito:

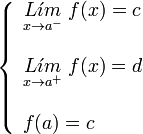
Referencias bibliograficas

www.vitutor.com/fun/3/b_5.html

www.vadenumeros.es › 1º Bachillerato