Unidad 3: Limites laterales

Limites laterales

El límte lateral por la derecha de una función y = f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores mayores que a .

Hasta el momento hemos visto límites de funciones cuyo trazo es continuo, sin cortes o saltos bruscos. Sin embargo, existen algunas funciones que presentan algunas discontinuidades, llamadas funciones discontinuas y que estudiaremos en el tema continuidad de funciones. Nos dedicaremos ahora a estudiar los límites en este tipo de funciones.
Consideremos la siguiente representación gráfica de una función 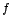, en la que existe una discontinuidad cuando :
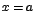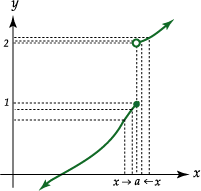notemos que cuando 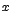tiende hacia "a" por la derecha de "a" la función tiende a 2, pero cuando 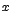tiende hacia "a" por la izquierda de "a", la función tiende hacia 1.


Escribimos 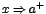para indicar que 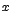tiende hacia "a" por la derecha, es decir, tomando valores mayores que "a". Similarmente 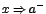indica que 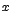tiende hacia "a" por la izquierda, o sea, tomando valores menores que "a". Utilizando ahora la notación de límites, escribimos 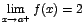y 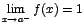. Estos límites reciben
el nombre de límites laterales; el límite por la derecha es 2 y el límite por la izquierda es 1.
Ejemplo:
Determinaremos los límites en los puntos de discontinuidad de la función 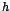cuya representación gráfica es la siguiente:
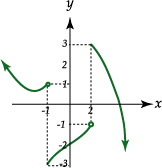Se tiene que:
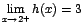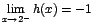
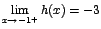y
y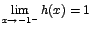

Referncias bibliograficas:
http://www.mat.uson.mx/~jldiaz/lim-laterales.html
https://darkcity2111.wordpress.com/3-5-limites-laterales/