Unidad 3: Limites infinitos y al infinito

Limites infinitos y limites al infinito 

LIMITES INFINITOS

Decimos que lim f(x)= si para los valores de x proximos a a,     x→ a    los valores de f(x) pueden hacerse tan grandes como queramos.

Con rigor, decimos que lim f(x)= si fijado a un valor k positivo y tan grande como se quisiera, existe un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entoces f(x)>k.

Análogamente,    lim f(x) = – 
x→a 

si para los valores de x cercanos a a, los valores de f(x) se pueden hacer tan pequeños como queramos.

Diremos que lim f(x) = – 
x→a 

si fijado un valor de k positivo y tan grande como se quisiera, podemos encontrar un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entonces  f(x) < -k

•Ejemplo:

la función f(x)= 1/|x|

En el punto x=0 se tiene:

lim 1/|x| = – 
x→ 0-
→ lim    1/|x| =                                                x→0 

lim 1/|x| = 
x→a’



El símbolo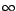  se lee infinito, es de carácter posicional, no representa ningún número real. 
Si una variable independiente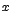  está creciendo indefinidamente a través de valores positivos, se escribe  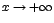(que se lee:  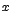tiende a más infinito), y si decrece a través de valores negativos, se denota como 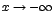(que se lee:  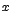tiende a menos infinito). 

¿Cuál es el límite de esta función?

y = 2x

Está claro que cuando "x" se hace más grande, le pasa lo mismo a "2x":

x	y=2x
1	2
2	4
4	8
10	20
100	200
...	...

Así que cuando "x" va a infinito, "2x" también va a infinito. Lo escribimos así:

Referencias bibliograficas
http://www.disfrutalasmatematicas.com/calculo/limites-infinito.html
https://calculolimitesycontinuidad.wordpress.com/limites-infinitos-limites-al-infinito/