Calculo de limites
Los límites son la herramienta principal sobre la que construimos el cálculo.
Muchas veces, una función puede no estar definida en un punto, pero podemos pensar a qué valor se aproxima la función mientras se acerca más y más a ese punto (esto es el límite).
Otras ocasiones, la función está definida en un punto, pero puede aproximarse a un límite diferente.
Hay muchas, muchas veces donde el valor de la función es el mismo que el del límite en el punto. De cualquier manera, esto es una poderosa herramienta cuando comenzamos a pensar en la pendiente de una recta tangente a una curva.
1) lim ------- = -- x->2 3x - 4 2 x2 - 1 3 2) lim -------- = -- = +inf x->2 x - 2 0 Factores Podemos probar factorizando. Ejemplo:Factorizando (x2-1) en (x-1)(x+1) tenemos:
Ahora sustituimos x=1 para calcular el límite:
3. Conjugar Si es una fracción, multiplicar arriba y abajo por un conjugado puede ayudar. El conjugado es cuando cambias el signo entre dos términos, así:
Aquí tienes un ejemplo en el que te ayuda a calcular un límite:
Evaluando en x=4 sale 0/0, ¡no es una respuesta válida! Así que vamos a manipular un poco: Multiplica arriba y abajo por el conjugado de lo de arriba:
Simplifica arriba usando
:
Simplifica arriba un poco más:
Elimina (4-x) arriba y abajo:
Así que nos queda:
Referencias bibliográficas: http://matematica.50webs.com/calculo-de-limites.html
http://www.disfrutalasmatematicas.com/calculo/limites-evaluacion.html
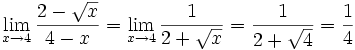
No hay comentarios:
Publicar un comentario