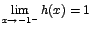Concepto de razon de cambio
Razón de cambio (de una variable respecto a otra) es la magnitud del cambio de una variable por unidad de cambio de la otra. (También se le llama tasa de cambio.) Si las variables no tienen ninguna dependencia la tasa de cambio es cero. En general, en una relación funcional y=f(x) , la razón de cambio de la variable dependiente y respecto a la independiente x se calcula mediante un proceso de límite --de la razón [f(x+t)−f(x)]/t , denominada cociente diferencial.
Concepto de incremento:[El incremento Dx de una variable x es el aumento o disminución que experimenta, desde un valor x = x0 a otro x = x1 de su campo de variación. Así, pues,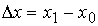

Derivada de una funcion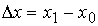

El concepto de derivada de una función matemática se halla íntimamente relacionado con la noción de límite. Así, la derivada se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.
Derivada de una función en un punto
Dada una función f (x), y considerado un punto a de su dominio, se llama derivada de la función en ese punto, denotada como f ¿ (a), al siguiente límite:

Este límite también puede expresarse de las dos formas alternativas siguientes:

Referencias bibliograficas
http://www.hiru.com/matematicas/derivada-de-una-funcion
https://sites.google.com/site/455laderivada/ejemplo-2




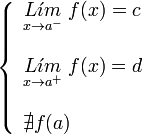

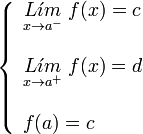






 es la asíntota horizontal.
es la asíntota horizontal.



 es la asíntota oblicua
es la asíntota oblicua
 si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos.
si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos. , en la que existe una discontinuidad cuando
, en la que existe una discontinuidad cuando  :
: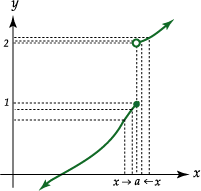 notemos que cuando
notemos que cuando 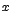 tiende hacia "a" por la derecha de "a" la función tiende a 2, pero cuando
tiende hacia "a" por la derecha de "a" la función tiende a 2, pero cuando 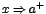 para indicar que
para indicar que 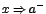 indica que
indica que 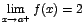 y
y 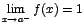 . Estos límites reciben
. Estos límites reciben 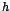 cuya representación gráfica es la siguiente:
cuya representación gráfica es la siguiente: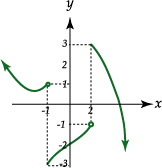 Se tiene que:
Se tiene que: 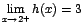 y
y 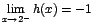
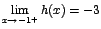 y
y