Funcion Inversa, Logaritmica y Trigonometrica
Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a) = b, entonces f−1(b) = a.
Veamos un ejemplo a partir de la función f(x) = x + 4

Podemos observar que:
El dominio de f−1 es el recorrido de f.El recorrido de f−1 es el dominio de f.Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.Si dos funciones son inversas su composición es la función identidad.
El dominio de f−1 es el recorrido de f.El recorrido de f−1 es el dominio de f.Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.Si dos funciones son inversas su composición es la función identidad.
(f o f−1) (x) = (f−1 o f) (x) = x
Ejercicios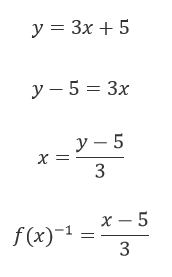
Ejercicios
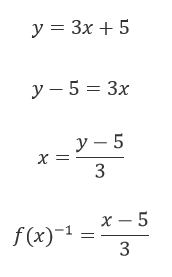
Ejercicio 2
f (x) =(3x + 2) / (2x – 5)
f (x) =(3x + 2) / (2x – 5)
Funcion Logaritmica
La función logarítmica en base a es la función inversa de la exponencial en base a.
La función logarítmica en base a es la función inversa de la exponencial en base a.



| x |  |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |

| x |  |
|---|---|
| 1/8 | 3 |
| 1/4 | 2 |
| 1/2 | 1 |
| 1 | 0 |
| 2 | −1 |
| 4 | −2 |
| 8 | −3 |
Funciones trigonométricas inversas
El arcoseno es la función inversa del seno. Es decir:

Al ser el arcoseno y el seno funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arcsen o sen-1.
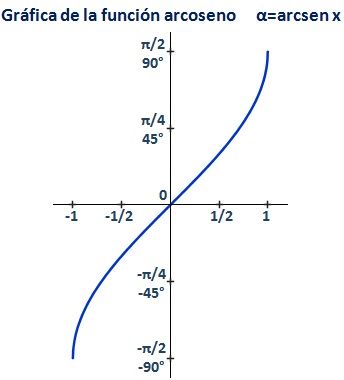
Dominio (x):

Codominio (α):

Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función seno no es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la función seno sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcoseno:

Arcoseno
El arcoseno es la función inversa del coseno. Es decir:

Al ser el arcocoseno y el coseno funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arccos o cos-1.

Dominio (x):

Codominio (α):

Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función coseno no esinyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [0,π] para que la funcióncoseno sea biyectiva.
La función es continua y decreciente en todo el dominio.
Derivada de la función arcocoseno:

Arcotangente
La arcotangente es la función inversa de la tangente. Es decir:

Al ser la arcotangente y la tangente funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arctan o tan-1.
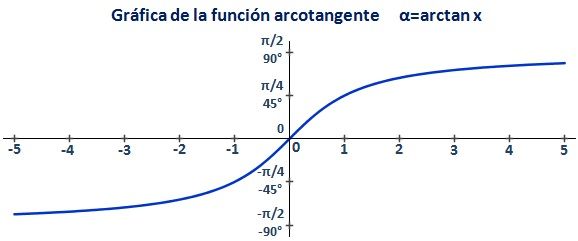
Dominio (x):
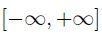
Codominio (α):

Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función tangente no esinyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la funcióntangente sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcotangente:

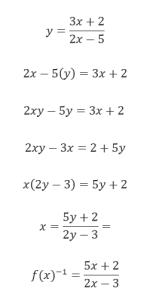
No hay comentarios:
Publicar un comentario