Nombre: Jorge Antonio Medina Narvaez
Escuela: Tecnologico de Matamoros
Fecha: 28/09/2015
Carrera: Ing. Mecatronica
Materia: Calculo Diferencial
No. de Control: 15260742
Unidad 1 Números Reales
Introducción
Un número es la expresión de una cantidad con relación a su unidad. El término proviene del latín numĕrus y hace referencia a un signo o un conjunto de signos. La teoría de los números agrupa a estos signos en distintos grupos. Los números naturales, por ejemplo, incluyen al uno (1), dos (2), tres (3), cuatro (4), cinco (5), seis (6), siete (7), ocho (8), nueve (9) y, por lo general, al cero (0)
1.1 La Recta Numérica
Todos los números pueden ordenarse en una recta numérica. De esta manera, podemos determinar si un número es mayor o menor que otro, dependiendo del lugar que ocupa en la recta numérica.
Decimos que un número es menor, cuando está ubicado a la izquierda de otro en la recta numérica, o sea, está más cerca del 0 y, decimos que es mayor, cuando se ubica a la derecha de otro y está más alejado del cero.
Localiza el punto de acuerdo a las desigualdades
A) 12>9 a>b
B A
B)3/4<5/4 a<b
A B
B A
|----|----|----|----|----|----|----|----|----|----|----|----|----|
-3 0 3 6 9 12 15 18 21 24 27 30 33 36B)3/4<5/4 a<b
A B
|------|------|------|------|------|------|------|------|
-3/4 -2/4 -1 0 1/4 2/4 3/4 4/4 5/4
-3/4 -2/4 -1 0 1/4 2/4 3/4 4/4 5/4
A B
C) (7)(2)<(3)(6) a<b |----|----|----|----|----|----|----|----|----|----|----|----|----|
0 2 4 6 8 10 12 14 16 18 20 22 24 26
14<18
D) (2)(3)/3< (2)(3)/2 |----|----|----|----|----|----|----|----|----|
2 < 3 -5 -4 -3 -2 -1 0 1 2 3 4
a<b
B A
E) 45>30/2 a>b |----|----|----|----|----|----|----|
-60 -45 -30 -15 0 15 30 45
a>b
A B
F) 20<10(3) a<b |----|----|----|----|----|----|----|
-30 -20 -10 0 10 20 30 40
a<b
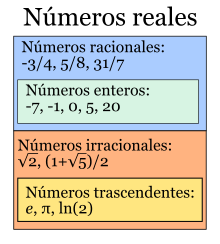
1.2 Los Números Reales
Los números reales (denotado por ℝ) incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes1 (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales a periódicas, tales como: √5, π, el número real log2, cuya trascendencia fue enunciada por Euler en el siglo XVIII.1
Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.
Ejercicios
Identifica la categoría de cada numero real representado
(a)Racional 1. (a ) -3/8
2. (b) π
(b) Irracional 3. (b) √2
4.(b) √5
5.(a) 1/7
6.(a) 10
7.(a) 28/1231
1.3 Propiedades de los Números Reales
A)Asigna a cada paréntesis con su propiedad
A) Conmutativa de la suma (A) . 2+3= 3+2
B) Asociativa de la suma (B). (2+3)+3=2(3+3)
C) Conmutativa de la multiplicación (C) (2)(3)=(2)(3)
D) Asociativa de la multiplicación (D) 4[(9)(8)]= 9[(4)(8)]
E) Elemento aditivo neutro (E) 9+0=9
F) Elemento neutro multiplicativo (F) (1432)(1)= 1432
G) Distributiva de la multiplicación con su propiedad (G) 9(2+3)= 9(2) + 9(3)
1.4 Intervalos y su representación mediante desigualdades
Una desigualdad es una expresión matemática que contiene un signo de desigualdad. Los signos de desigualdad son:
≠ no es igual
< menor que
> mayor que
≤ menor o igual que
≥ mayor o igual que
De la definición de desigualdad, lo mismo que de la escala de los números algebraicos, se deducen algunas consecuencias, a saber:
1º Todo número positivo es mayor que cero
1)Ejemplo:
5>x > 0 ; porque 5 – 0 = 5Intervalo
(5>x>0)
2º Todo número negativo es menor que cero
–9<x < 0 ; porque –9 –0 = –9
Intervalos
(-9<x<0)
3º Si dos números son negativos, es mayor el que tiene menor valor absoluto;
Intervalos
2)Ejemplo:
–9<x < 0 ; porque –9 –0 = –9
Intervalos
(-9<x<0)
3º Si dos números son negativos, es mayor el que tiene menor valor absoluto;
3)Ejemplo:
–10 > –30; porque -10 – (–30) = –10 +30 = 20Intervalos
(-10>x>-30)
Una desigualdad que contiene al menos una variable se llama inecuación.
4)Por ejemplo:
X + 3 < 7(La punta del signo < siempre señala el menor)
Ejemplos:
3 < 4, 4 > 3
¿Cómo resolvemos una inecuación? Para esto tenemos que conocer y entender las propiedades de las desigualdades.
Propiedades de las desigualdades
1. Una desigualdad no varía si se suma o resta la misma cantidad a ambos lados:
a < b / ± c (sumamos o restamos c a ambos lados)
a ± c < b ± c
5)Ejemplo:
2 + x > 16 / – 2 (restamos 2 a ambos lados)2 + x − 2 > 16 − 2
x > 14
Intervalo
(14<x<+infinito)
2. Una desigualdad no varía su sentido si se multiplica o divide por un número positivo:
a < b / • c (c > 0) (c es positivo, mayor que cero)
a • c < b • c
a > b / • c (c > 0) (c es positivo, mayor que cero)
a • c > b • c
6)Ejemplo
3 ≤ 5 • x / :53/5 ≤ x esto es, todos los reales mayores o iguales que 3/5
Intervalo
[3/5<x<+infinito)
3. Una desigualdad varía su sentido si se multiplica o divide por un número negativo:
a < b / • c (c < 0) (c es negativo, menor que cero)
a • c > b • c
a > b / • c (c < 0) (c es negativo, menor que cero)
a • c < b • c
7)Ejemplo:
15 – 3 • x ≥ 39 / −15− 3 • x ≥ 39 – 15 /: −3
x ≤ 24: (−3)
x ≤ − 8. Esto es, todos los reales menores o iguales que −8.
Intervalo
(-infinito<x≤ − 8]
De manera recíproca, cuando la parte de la incógnita resulta negativa deben invertirse los signos a ambos lados y cambiar el sentido de la desigualdad, ya que no puede haber desigualdades con incógnita negativa.
1.5 Resolución de desigualdades de primer grado con una incógnita y de desigualdades cuadráticas con una incógnita
Sumamos 5 a los dos lados de la desigualdad
3x – 5 + 5 ≥ 5x + 15 + 5
3x ≥ 5x + 20
Restamos 5x en ambos lados
3x – 5x ≥ 5x + 20 – 5x
-2x ≥ 20
Multiplicamos ambos lados por -1/2 *
-1/2(-2x) ≤ -1/2(20)
x ≤ -10
* La dirección de la desigualdad cambia al multiplicar por un número negativo.
El resultado es el intervalo (-∞ , -10]
(1/3)x + 1/2 < -2x + 1
Restamos 1/2 a los dos lados
(1/3)x + 1/2 – 1/2 < -2x + 1 – 1/2
(1/3)x < -2x + 1/2
Sumamos 2x en ambos lados
(1/3)x + 2x < -2x + 1/2 + 2x
(7/3)x < 1/2
Multiplicamos a los dos lados por 3/7
3/7(7/3)x < 3/7(1/2)
x < 3/14
Nótese que en este caso no hubo cambio de dirección de la desiguladad por que la multiplicación fue por un número positivo.
El resultado es el intervalo (-∞ , 3/14)
x2 > 3x + 4
Primero expresamos la desigualdad como una ecuación y resolvemos.
x2 = 3x + 4
Restamos (3x + 4) a los dos lados para que uno de los lados quede con valor cero.
x2 – (3x + 4) = 3x + 4 – (3x + 4)
x2 – 3x – 4 = 0
Como obtuvimos un trinomio cuadrado, lo podemos resolver por fórmula general o por factorización. En este caso utilizaremos la factorización.
(x + 1)(x – 4) = 0
Separamos cada uno de los factores y los solucionamos
Primer factor
x + 1 = 0
x1 = -1
Segundo factor
x – 4 = 0
x2 = 4



P(−3) = 4 · (−3)2 − 16 > 0
P(0) = 4 · 0 2 − 16 < 0
P(3) = 4 · 3 2 − 16 > 0

(-∞ , −2] [2, +∞)
[2, +∞)
4x2 − 4x + 1 ≤ 0
4x2 − 4x + 1 = 0


El valor absoluto de un número real a coincide con él mismo si es positivo ó 0, y es igual a su opuesto si es negativo. Se representa por |a|.
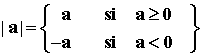
De modo que el valor absoluto de cualquier número nunca es negativo.
El valor absoluto de un número coincide siempre con el de su opuesto.
a) |3,5| = 3,5
b) |-1,6| = 1,6
c) |4 - 9| = |-5| = 5
d) |π - 2| = π - 2 = 1,141...
Propiedades del valor absoluto
1. |-7| = |7| =7
2. |(-2) · 5| = |-10| = 10 = |-2| · |5| = 2 · 5
3. |4 + 2| = |6| = 6 = |4| + |2|
Igualmente:
|4 + (-2)| = |2| = 2 ≤ |4| + |-2| = 4 + 2 = 6
4. Si |3|<4, entonces -4 < 3 < 4
Observaciones de las propiedades del valor absoluto
|x| = a son los valores x tales que x = a o x = - a
|x| < a son los valores x tales que - a < x < a
|x| > a son los valores x tales que x < - a o x > a
La desigualdad |x| ≤ a describe el intervalo cerrado [-a , a] , simétrico respecto al origen.
Y los números reales |x| < a son los del intervalo abierto (-a, a).
La desigualdad |x| ≥ a describe la unión de los intervalos (-∞ , -a] ∪ [a , ∞).
Y los números reales |x| > a son la unión de los intervalos abiertos (-∞ , -a) ∪ (a , ∞).
La desigualdad |x - c| < d es el intervalo abierto (c - d , c + d) , denominado también entorno de centro c y radio d, E(c , r).
La desigualdad |x - c| ≤ d es el intervalo cerrado [c - d , c + d].
La desigualdad |x - c| > d es la unión de los intervalos (-∞ , c - d) ∪ (c + d , ∞).
La desigualdad |x - c| ≥ d es la unión de los intervalos (-∞ , c - d] ∪ [c + d , ∞).
1.7 Resolución de desigualdades que incluyan valor absoluto
 .
.
Utilizando la propiedad (6), tenemos la siguiente cadena de desigualdades equivalentes:

Por lo tanto, la solución de la desigualdad es el intervalo .
.
Resolvamos la desigualdad .
.
La propiedad (7) nos dice que la desigualdad es equivalente a

Resolviendo

o sea

Por lo tanto, la solución de la desigualdad dada es
 .
.
Utilizando la propiedad (8) del valor absoluto, tenemos la siguiente cadena de desigualdades equivalentes:

Elaborando un diagrama de signos tenemos
Signo de + - -
+ - -
Signo de - - +Signo de
- - +Signo de  - + -
- + -
Vemos que la solución de la desigualdad es .
.
Resuelva y grafique.
|x – 7| < 3
Para resolver este tipo de desigualdad, necesitamos descomponerla en una desigualdad compuesta.
x – 7 < 3 Y x – 7 > –3
–3 < x – 7 < 3
Sume 7 en cada expresión.
-3 + 7 < x - 7 + 7 < 3 + 7
4 < x <10
La gráfica se vería así:

La desigualdad | x | > 4 significa que la distancia entre x y 0 es mayor que 4.

Así, x < -4 O x > 4. El conjunto solución es .
.
Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
En otras palabras, para cualesquiera numéros reales a y b , si | a | > b, entonces a > b O a < - b .
La desigualdad | x | > 4 significa que la distancia entre x y 0 es mayor que 4.

Así, x < -4 O x > 4. El conjunto solución es .
.
Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
En otras palabras, para cualesquiera numéros reales a y b , si | a | > b, entonces a > b O a < - b .

Referencias:
http://calculo.cc/N%C3%BAmeros_reales/Valor_absoluto.html
http://www.vitutor.com/ecuaciones/ine/s_e.html
http://www.vadenumeros.es/cuarto/resolver-inecuaciones.htm
De manera recíproca, cuando la parte de la incógnita resulta negativa deben invertirse los signos a ambos lados y cambiar el sentido de la desigualdad, ya que no puede haber desigualdades con incógnita negativa.
1.5 Resolución de desigualdades de primer grado con una incógnita y de desigualdades cuadráticas con una incógnita
1)Ejemplo
3x – 5 ≥ 5x + 15Sumamos 5 a los dos lados de la desigualdad
3x – 5 + 5 ≥ 5x + 15 + 5
3x ≥ 5x + 20
Restamos 5x en ambos lados
3x – 5x ≥ 5x + 20 – 5x
-2x ≥ 20
Multiplicamos ambos lados por -1/2 *
-1/2(-2x) ≤ -1/2(20)
x ≤ -10
* La dirección de la desigualdad cambia al multiplicar por un número negativo.
El resultado es el intervalo (-∞ , -10]
2)Ejemplo
(1/3)x + 1/2 < -2x + 1
Restamos 1/2 a los dos lados
(1/3)x + 1/2 – 1/2 < -2x + 1 – 1/2
(1/3)x < -2x + 1/2
Sumamos 2x en ambos lados
(1/3)x + 2x < -2x + 1/2 + 2x
(7/3)x < 1/2
Multiplicamos a los dos lados por 3/7
3/7(7/3)x < 3/7(1/2)
x < 3/14
Nótese que en este caso no hubo cambio de dirección de la desiguladad por que la multiplicación fue por un número positivo.
El resultado es el intervalo (-∞ , 3/14)
3)Ejemplo
x2 > 3x + 4
Primero expresamos la desigualdad como una ecuación y resolvemos.
x2 = 3x + 4
Restamos (3x + 4) a los dos lados para que uno de los lados quede con valor cero.
x2 – (3x + 4) = 3x + 4 – (3x + 4)
x2 – 3x – 4 = 0
Como obtuvimos un trinomio cuadrado, lo podemos resolver por fórmula general o por factorización. En este caso utilizaremos la factorización.
(x + 1)(x – 4) = 0
Separamos cada uno de los factores y los solucionamos
Primer factor
x + 1 = 0
x1 = -1
Segundo factor
x – 4 = 0
x2 = 4
4)Ejemplo
x2 − 6x + 8 > 0
x2 − 6x + 8 = 0

7x2 + 21x − 28 < 0
x2 +3x − 4 < 0
x2 +3x − 4 = 0

P(−6) = (−6)2 +3 · (−6)− 4 > 0
P(0) = 02 +3 · 0 − 4 < 0
P(3) = 32 +3 · 3 − 4 > 0

(−4, 1)
x2 − 6x + 8 = 0

5)Ejemplo
7x2 + 21x − 28 < 0
x2 +3x − 4 < 0
x2 +3x − 4 = 0

P(−6) = (−6)2 +3 · (−6)− 4 > 0
P(0) = 02 +3 · 0 − 4 < 0
P(3) = 32 +3 · 3 − 4 > 0

(−4, 1)
6)Ejemplo



P(−3) = 4 · (−3)2 − 16 > 0
P(0) = 4 · 0 2 − 16 < 0
P(3) = 4 · 3 2 − 16 > 0

(-∞ , −2]
 [2, +∞)
[2, +∞)
7) Ejemplo
4x2 − 4x + 1 ≤ 0
4x2 − 4x + 1 = 0


1.6 Valor Absoluto y sus propiedades
El valor absoluto de un número real a coincide con él mismo si es positivo ó 0, y es igual a su opuesto si es negativo. Se representa por |a|.
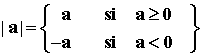
De modo que el valor absoluto de cualquier número nunca es negativo.
El valor absoluto de un número coincide siempre con el de su opuesto.
Ejemplos de valor absoluto
a) |3,5| = 3,5
b) |-1,6| = 1,6
c) |4 - 9| = |-5| = 5
d) |π - 2| = π - 2 = 1,141...
Propiedades del valor absoluto
Ejemplos de las propiedades del valor absoluto
1. |-7| = |7| =7
2. |(-2) · 5| = |-10| = 10 = |-2| · |5| = 2 · 5
3. |4 + 2| = |6| = 6 = |4| + |2|
Igualmente:
|4 + (-2)| = |2| = 2 ≤ |4| + |-2| = 4 + 2 = 6
4. Si |3|<4, entonces -4 < 3 < 4
Observaciones de las propiedades del valor absoluto
|x| = a son los valores x tales que x = a o x = - a
|x| < a son los valores x tales que - a < x < a
|x| > a son los valores x tales que x < - a o x > a
La desigualdad |x| ≤ a describe el intervalo cerrado [-a , a] , simétrico respecto al origen.
Y los números reales |x| < a son los del intervalo abierto (-a, a).
La desigualdad |x| ≥ a describe la unión de los intervalos (-∞ , -a] ∪ [a , ∞).
Y los números reales |x| > a son la unión de los intervalos abiertos (-∞ , -a) ∪ (a , ∞).
La desigualdad |x - c| < d es el intervalo abierto (c - d , c + d) , denominado también entorno de centro c y radio d, E(c , r).
La desigualdad |x - c| ≤ d es el intervalo cerrado [c - d , c + d].
La desigualdad |x - c| > d es la unión de los intervalos (-∞ , c - d) ∪ (c + d , ∞).
La desigualdad |x - c| ≥ d es la unión de los intervalos (-∞ , c - d] ∪ [c + d , ∞).
1.7 Resolución de desigualdades que incluyan valor absoluto
1)Resolvamos la desigualdad
 .
.Utilizando la propiedad (6), tenemos la siguiente cadena de desigualdades equivalentes:

Por lo tanto, la solución de la desigualdad es el intervalo
 .
.
2)Ejemplo.
Resolvamos la desigualdad
 .
.La propiedad (7) nos dice que la desigualdad es equivalente a

Resolviendo

o sea

Por lo tanto, la solución de la desigualdad dada es

3)Ejemplo.
Resolvamos la desigualdad  .
.Utilizando la propiedad (8) del valor absoluto, tenemos la siguiente cadena de desigualdades equivalentes:

Elaborando un diagrama de signos tenemos
Signo de
 + - -
+ - -Signo de
 - - +Signo de
- - +Signo de  - + -
- + -Vemos que la solución de la desigualdad es
 .
.
Ejemplo 4:
Resuelva y grafique.
|x – 7| < 3
Para resolver este tipo de desigualdad, necesitamos descomponerla en una desigualdad compuesta.
x – 7 < 3 Y x – 7 > –3
–3 < x – 7 < 3
Sume 7 en cada expresión.
-3 + 7 < x - 7 + 7 < 3 + 7
4 < x <10
La gráfica se vería así:

Ejemplo 5)Desigualdades de valor absoluto (>):

Así, x < -4 O x > 4. El conjunto solución es
 .
.Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
En otras palabras, para cualesquiera numéros reales a y b , si | a | > b, entonces a > b O a < - b .
Ejemplo 6)Desigualdades de valor absoluto (>):
La desigualdad | x | > 4 significa que la distancia entre x y 0 es mayor que 4.

Así, x < -4 O x > 4. El conjunto solución es
 .
.Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
En otras palabras, para cualesquiera numéros reales a y b , si | a | > b, entonces a > b O a < - b .
Ejemplo numero 7

Referencias:
http://calculo.cc/N%C3%BAmeros_reales/Valor_absoluto.html
http://www.vitutor.com/ecuaciones/ine/s_e.html
http://www.vadenumeros.es/cuarto/resolver-inecuaciones.htm
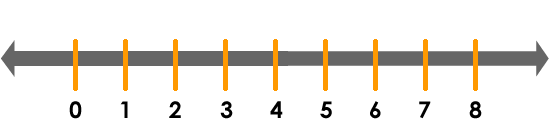

No hay comentarios:
Publicar un comentario