Introduccion
Para dar inicio a la nueva unidad , antes se deben conocer o reafirmas algunos conceptos los cuales se describiran en el primer punto de este blog , espero sea comprensible y de su agrado
2.1 Concepto de una Variable , Funcion , Dominio , Codominio y Recorrido de una funcion
2.1 Concepto de una Variable , Funcion , Dominio , Codominio y Recorrido de una funcion
Variable
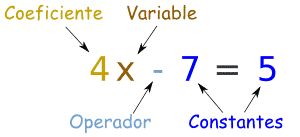La matemática se destaca como ámbito del uso de las variables: están presentes en fórmulas, proposiciones y algoritmos. También se ve la idea de variables independientes y dependientes, destacándose las funciones matemáticas que permiten la conformación de gráficos de dos o más ejes: la relación entre esos dos ejes viene dada por una función en la que uno de los dos es variable en función del otro, que es invariable (Y es igual a la mitad de X, tiene a Y como variable dependiente y a X como independiente).
En la estadística se utiliza también la variable en el sentido matemático, encarada desde la misma perspectiva: al ser medida en diferentes casos adopta distintos valores. Una clasificación interna divide a las variables estadísticas según expresen cantidades numéricas (variables cuantitativas o continuas) o expresen características, cualidades o modos de comportamiento (variables cualitativas o discretas).
- Ejercicios:
2x+3=5 Variable- X
2b+3a-2c=0 Variables= a,b,c
En la estadística se utiliza también la variable en el sentido matemático, encarada desde la misma perspectiva: al ser medida en diferentes casos adopta distintos valores. Una clasificación interna divide a las variables estadísticas según expresen cantidades numéricas (variables cuantitativas o continuas) o expresen características, cualidades o modos de comportamiento (variables cualitativas o discretas).
- Ejercicios:
2x+3=5 Variable- X
2b+3a-2c=0 Variables= a,b,c
Funcion
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamadocodominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman elrecorrido, también llamado rango o ámbito).
En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.
Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.
A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
Los números de la derecha son los cuadrados de los de la izquierda.
La regla es entonces "elevar al cuadrado"
Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota
f : A -----> B (o, usando X por A e Y por B f : X -----> Y) o f(x) = x
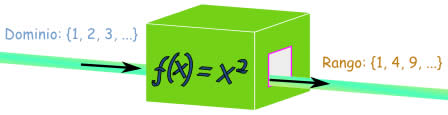
Dominio
El conjunto de todos los posibles valores de ingreso que la función acepta.
Cuando nos hemos referido al dominio hemos dicho: “conjunto de valores quepuede tomar x…” ¿por qué decimos puede?
Porque no todos los valores son válidos, por ejemplo, si la función es: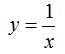 
vemos que si a x le das el valor cero, te queda: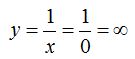 
El valor infinito no lo podemos representar si no es con un signo o una palabra.
El infinito no es un número, es un concepto, una idea, luego, no nos vale como valor numérico de y.
Otro caso sería el de la función: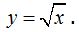
A x no le podemos dar el valor de un número negativo, por ejemplo: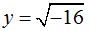 
porque los números negativos no tienen raíz cuadrada. (Ningún número multiplicado por sí mismo -incluido su signo- puede darte un valor negativo).
Codominio o recorrido
El codominio es el conjunto de valores que podrían salir.
El rango es el conjunto de valores que realmente salen.
El codominio de una función también es un conjunto, y seguramente ya estás deduciendo el concepto a partir de los puntos anteriormente abordados. De hecho, el codominio de una función, es lo que llamamos el conjunto de “llegada” es decir, el conjunto del que forman parte aquellos elementos resultantes de la interacción del conjunto de partida con su participación en la función.
Veamos la tabla de valores de la función anterior, expresada en un diagrama de Venn:
El dominio son todos los Números reales, de los cuales hemos utilizado algunos que vemos en el diagrama de la izquierda; el codominio también son los Números reales, y entre ellos, llamamos imagen o rango a aquellos que terminan siendo efectivamente resultado de la función, en este caso serían -3, -1, 0, 1, 5 y 7.
Cuando nos hemos referido al dominio hemos dicho: “conjunto de valores quepuede tomar x…” ¿por qué decimos puede?
Porque no todos los valores son válidos, por ejemplo, si la función es:
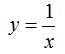vemos que si a x le das el valor cero, te queda: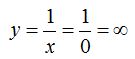 El valor infinito no lo podemos representar si no es con un signo o una palabra.
El infinito no es un número, es un concepto, una idea, luego, no nos vale como valor numérico de y.
Otro caso sería el de la función:
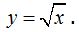
A x no le podemos dar el valor de un número negativo, por ejemplo:
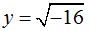porque los números negativos no tienen raíz cuadrada. (Ningún número multiplicado por sí mismo -incluido su signo- puede darte un valor negativo).
El codominio es el conjunto de valores que podrían salir.
El rango es el conjunto de valores que realmente salen.
El codominio de una función también es un conjunto, y seguramente ya estás deduciendo el concepto a partir de los puntos anteriormente abordados. De hecho, el codominio de una función, es lo que llamamos el conjunto de “llegada” es decir, el conjunto del que forman parte aquellos elementos resultantes de la interacción del conjunto de partida con su participación en la función.
Veamos la tabla de valores de la función anterior, expresada en un diagrama de Venn:
El dominio son todos los Números reales, de los cuales hemos utilizado algunos que vemos en el diagrama de la izquierda; el codominio también son los Números reales, y entre ellos, llamamos imagen o rango a aquellos que terminan siendo efectivamente resultado de la función, en este caso serían -3, -1, 0, 1, 5 y 7.
No hay comentarios:
Publicar un comentario