Unidad 2: 2.10 Funciones Implicitas

Funcion Implicita

Unidad 2 : Funciones - 2.9 Funciones con dominio en los numeros naturales y recorrido en los numeros reales: las sucesiones infinitas

 Funciones con dominio en los numeros naturales y recorrido en los numeros reales: las  sucesiones infinitas

Funciones con Dominio en los Números Naturales y un Viaje a los Números Reales: Las Secuencias Infinitas

Considere un conjunto N, una función f: X  Y de la secuencia de números de N esta es conocida como función de sucesiones. El dominio de tales funciones se limita sólo a los números naturales. Las convenciones utilizadas para referirse a tales secuencias son,
o o


La notación convenida para denotar una función de este tipo sería,



Una secuencia infinita puede ser definida como un conjunto ordenado o una lista de elementos distintos que pueden ser formados como pares teniendo correspondencia uno a uno respecto al conjunto entero positivo. Los elementos son por lo general números. Un conjunto de números naturales es un buen ejemplo de sucesión infinita, N = {0, 1, 2, 3, 4…}.


Una secuencia decreciente infinita es opuesta a la sucesión creciente infinita lo que significa que en el caso de una secuencia decreciente infinita el elemento subsecuente de la secuencia es más pequeño que el elemento que estaba ocurriendo antes que este en la secuencia, esto es un an+1 < an para todos los valores de n.

Mientras que una secuencia infinita monótona puede ser una que esté creciendo o decreciendo.

Otra categoría en la que una secuencia puede ser clasificada está basada en los límites de la secuencia, si estos se encuentran por encima o por debajo. Si existe un número M para el cual an <= M, para todos los valores de n, entonces tal secuencia está limitada por encima. Mientras que si an >= M, para todos los valores de n, entonces tal secuencia está limitada por debajo.

También existen dos vías de secuencias infinitas o secuencia infinita-bi, la cual es una función del conjunto de todos los enteros en otro conjunto.

Supongamos una función f: {1, 2, 3, 4…}  {1, 2, 3, 4…} define una secuencia A donde cada ai = f(i). Tal secuencia se denominaría multiplicativa cuando,

f(xy) = f(x) f(y), para todos los valores de x e y, donde x e y son co-primos.

Una serie es la sumatoria de la suma de todos los elementos de una secuencia. La suma de todos los elementos de una secuencia infinita se denomina serie infinita.

Unidad 2; Funciones- 2.8 Funcion Inversa , Logaritmica y Trigonométrica

Funcion Inversa, Logaritmica y Trigonometrica

Se llama función inversa o reciproca de f a otra función f⁻¹ que cumple que:

Si f(a) = b, entonces f⁻¹(b) = a.

Veamos un ejemplo a partir de la función f(x) = x + 4

Podemos observar que:
El dominio de f⁻¹ es el recorrido de f.El recorrido de f⁻¹ es el dominio de f.Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.Si dos funciones son inversas su composición es la función identidad.

(f o f⁻¹) (x) = (f⁻¹ o f) (x) = x

Ejercicios

Ejercicio 2 
f (x) =(3x + 2) / (2x – 5)

 Funcion Logaritmica
La función logarítmica en base a es la función inversa de la exponencial en base a.

x
1/8	-3
1/4	-2
1/2	-1
1	0
2	1
4	2
8	3

x
1/8	3
1/4	2
1/2	1
1	0
2	−1
4	−2
8	−3

Funciones trigonométricas inversas

El arcoseno es la función inversa del seno. Es decir:







Al ser el arcoseno y el seno funciones inversas, su composición es la identidad, es decir:







Su abreviatura es arcsen o sen-1.






Dominio (x):
Codominio (α):

Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función seno no es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la función seno sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcoseno:
Arcoseno

El arcoseno es la función inversa del coseno. Es decir:







Al ser el arcocoseno y el coseno funciones inversas, su composición es la identidad, es decir:







Su abreviatura es arccos o cos-1.






Dominio (x):
Codominio (α):

Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función coseno no esinyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [0,π] para que la funcióncoseno sea biyectiva.
La función es continua y decreciente en todo el dominio.
Derivada de la función arcocoseno:
Arcotangente

La arcotangente es la función inversa de la tangente. Es decir:







Al ser la arcotangente y la tangente funciones inversas, su composición es la identidad, es decir:







Su abreviatura es arctan o tan-1.






Dominio (x):
Codominio (α):

Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función tangente no esinyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la funcióntangente sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcotangente:

Unidad 2 : Funciones 2.7 Operaciones con funciones; condicion , multiplicacion , composicion

Operaciones con Funciones

Suma de funciones

Sean f y g dos funciones reales de variable real definidas en un mismo intervalo. Se llama suma de ambas funciones, y se representa por f + g, a la función definida por







Resta de funciones

Del mismo modo que se ha definido la suma de funciones, se define la resta de dos funciones reales de variable real f y g, como la función







Para que esto sea posible es necesario que f y g estén definidas en un mismo intervalo.



Producto de funciones

Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por







Cociente de funciones

Dadas dos funciones reales de variable real, f y g, y definidas en un mismo intervalo, se llama función cociente de f y g a la función definida por







(La función f/g está definida en todos los puntos en los que la función g no se anula.)



Producto de un número por una función

Dado un número real a y una función f, el producto del número por la función es la función definida por









Ejercicio:

 Sean las funciones f(x) = 3x + 1, y g(x) = 2x - 4.



Resolución:


· La función f + g se define como

(f + g) (x) = f(x) + g(x) = 3x + 1 + 2x - 4 = 5x - 3.

Resolucion

 La función f - g se define como

(f - g) (x) = f(x) - g(x) = 3x + 1 - 2x + 4 = -x + 5.
·

Unidad 2: Funciones - 2.6 Funcion Definida por mas de una regla de correspondencia , funcin de valor absoluto

Función Definida Por Mas de Una Regla De Correspondencia 

Función a trozos es un nombre más general para una función que puede ser definida con la ayuda de múltiples funciones de correspondencia.
Una función f: X → Y es llamada una función a trozos si puede ser definida con la ayuda de varias funciones lineales.
Podemos decir que tal función está definida en una serie de intervalos múltiples.


La notación general para definir una función a trozos es la siguiente:


Como se muestra en el ejemplo, punto y coma o comas se utilizan al final de la columna.
Sin embargo, algunos los autores prefieren usar palabras como “si” o “para” en la columna derecha, y la palabra “ de lo contrario” también se puede utilizar para indicar el caso por defecto.
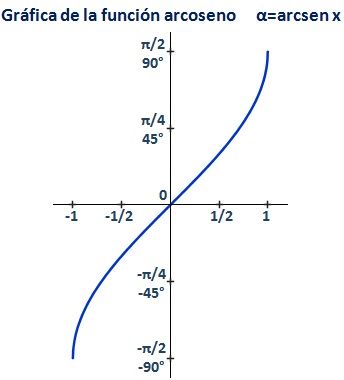
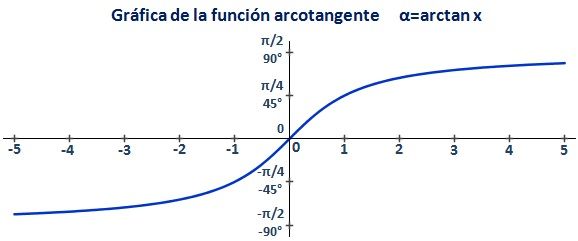
La gráfica de esta función también se divide en trozos, dependiendo del número de ecuaciones que se utilicen para definir la función.
Tal función es llamada de esta forma porque la definición de esta función cambia dependiendo del valor de la variable de entrada.
Aquí el uso de la palabra “a trozos” se hace para describir la propiedad de esa función, que es válida para una ecuación / pieza de la función pero no en todo el dominio de la función.
La función a trozos tiene una serie de funciones en su cuerpo, el dominio de cada una de ellas se define por separado.


Función valor absoluto:
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
3. Definimos la función a trozos, teniendo en cuanta que en los intervalos donde la x es negativa se cambia el signo de la función.
4. Representamos la función resultante.

Ejemplo

             

Ejemplo
2. 

Unidad 2: Funciones-2.5 Funciones Trascendentes

Funciones Trascendentes

En las funciones trascendentes la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

Las funciones que no son algebraicas se llaman funciones trascendentes.



Son funciones trascendentales elementales
Función exponencial:

f(x)=ax; a > 0, a ≠ 1.

Función logarítmica:

f(x)=loga(x); a > 0, a ≠ 1. Es inversa de la exponencial.

Funciones trigonométricas:

También llamadas circulares

f(x)=sen(x); f(x)=cos(x); f(x)=tg(x); f(x)=cosec(x); f(x)=sec(x) y f(x)=cotg(x)

Hay otras funciones elementales como las hiperbólicas y las inversas de éstas y de las trigonométricas, pero no pretendemos en esta unidad didáctica presentarlas todas y más bien analizar algunos casos, no excesivamente complicados, donde intervengan las primeras.

Debemos de tener en cuenta las siguientes observaciones para la hora de analizar las funciones trascendentes que se proponen en esta unidad didáctica:


f(x)=a^x está definida para todo x en R


f(x)=a^-x=(1/a)x, a>1, 0<1/a<1


f(x)=loga(x) está definida para x>0


Representaremos el logaritmo decimal log10(x) por log(x) y el logaritmo neperiano loge(x) por ln(x), siendo e=2,718281... el llamado número 'e'


f(x)=sen(x) y f(x)=cos(x) están definidas para todo valor de x. Su periodo es 2(3.1416)


Identificar:

f(x)=20^x  (exponencial)


f(x)= x^20    (potencia)