Unidad 4: Interpretación geométrica de la derivada

  

Se representa la posición de las distintas rectas AP (recta que une los puntos de abscisa a y a+h en la función f(x)) cuando el incremento de la variable h tiende a 0. 

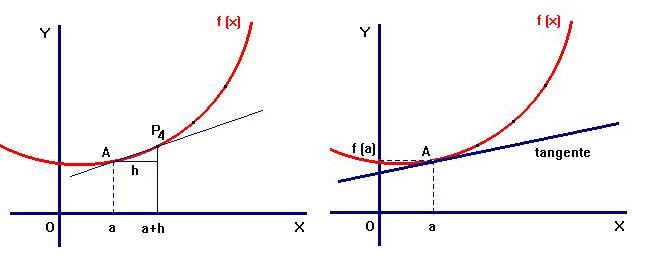
Interpretación geométrica de la derivada

Observamos que a medida que h se hace mas pequeño los puntos P₁,P₂,P₃,P₄ .. se aproximan al punto A y las rectas secantes AP₁,AP₂,AP₃,AP₄... tienden a la recta tangente. Las rectas AP₁,AP₂,AP₃, AP₄ que pasan por el punto A quedan determinadas por su pendiente. Esa pendiente es la tasa de variación media.

Por tanto, la pendiente de la recta tangente a la función f(x) en el punto A es:

m =   lim⁡ h→0   f ( a + h) - f (a) h  = f ' (a)  
La pendiente de la recta tangente a f(x) en x = a coincide con la derivada en x = a

Como el punto A tiene de coordenadas (a, f(a)), la ecuación de la recta tangente en el punto A a la función f(x) es: 

y - f(a) = f '(a) ( x - a)

Ejemplo

Ejemplo 2

Halla la ecuación de la recta tangente a la curva  en el punto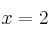 

La fórmula es 

Referencia bibliográfica:
http://www.lemat.unican.es/lemat/proyecto_lemat/derivadas/nivel1/teoria/derivadas6.htm
http://matematicasies.com/Interpretacion-geometrica-de-la