Calculo Diferencial: 2015

martes, 1 de diciembre de 2015

Unidad 4: Derivadas implicitas

DERIVADA DE FUNCIONES IMPLÍCITAS
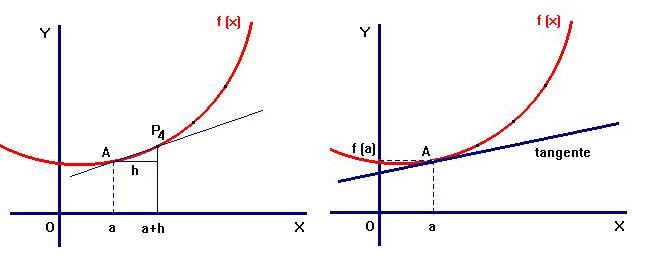
Función en forma explícita:

Función en forma implícita: y² + x² = 5
Procedimiento para derivar una función implícita:
Paso 1. Se deriva cada término con respecto a x
Paso 2. Se despeja dx/dy
Paso 3. De la ec. original (si es posible) se despeja y
Paso 4. Se sustituye en la solución. (En general, los resultados de las funciones implícitas incluyen a x y a y)

Funciones implícitas

Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.

Ejemplo 1. Derivar la función implícita x² + y² = 5
Paso 1.

Paso 2.

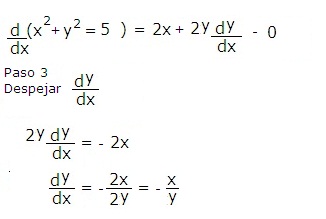
Pas4.
De la ec. original( si es posible) se despeja y, enseguida se sustituye en la solución:

Unidad 4: Derivadas de orden superior y regla de L Hopital

Derivadas de orden superior

es una función diferenciable, es posible considerar su función derivada como:
$f'=\{(x,y)/\;y=D_{x}f(x)\}$ para

en el dominio

.
Si para algunos valores $x \in M$ existe el $\displaystyle{\lim_{h \rightarrow{0}}{\frac{f'(x+h)-f'(x)}{h}}}$ se dice que existe la segunda derivada de la función

que se denota por

o $D_{x}^{2}f(x)$ , que equivale a $D_{x}[D_{x}f(x)]$ . O sea, la segunda derivada de la función

se obtiene derivando la primera derivada de la función.
Ejemplos:

Si $f(x)=5x^{3}+6x^{2}-5x+1$ entonces:
$f'(x)=15x^{2}+12x-5$ y
Si $\displaystyle{g(x)=\frac{x^{2}+3x}{x-1}}$ entonces:
$\displaystyle{g'(x)=\frac{(x-1)(2x+3)-(x^{2}+3x)}{(x-1)^{2}}=\frac{x^{2}-2x-3}{(x-1)^{2}}}$ y derivando nuevamente
$\displaystyle{g''(x)=\frac{(x-1)^{2}(2x-2)-(x^2-2x-3)2(x-1)}{(x-1)^{4}}}$
$=\displaystyle{\frac{(x-1)^{2}(2x-2)-(x^{2}-2x-3)2(x-1)}{(x-1)^{4}}}$
$=\displaystyle{\frac{(x-1)[(x-1)(2x-2)-(x^{2}-2x-3)]}{(x-1)^{4}}}$
Por tanto $\displaystyle{g''(x)=\frac{8}{(x-1)^{3}}}$

Regla de L'Hôpital para límites.

La regla de L´Hôpital permite resolver muchos casos de indeterminación de límites de funciones en un punto x = a. En principio la vamos a enunciar así:

Un límite indeterminado de la forma:

valdrá L, en caso de que también sea L el límite en x=a del cociente de las derivadas de numerador y denominador, es decir:

De esta manera podemos resolver indeterminaciones del tipo 0/0. Veamos un ejemplo.

EJEMPLO 1: Hallar el límite:

este límite tiene la forma indeterminada 0/0, por tanto, podemos aplicar la regla de L'Hôpital:

límite que sigue teniendo la forma indeterminada 0/0, pero a la cual se puede volver a aplicar la regla de L'Hôpital:

Referencia bibliografica:
http://www.ehu.eus/juancarlos.gorostizaga/apoyo/lim_lhopital.htm
https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/node11.html

Unidad 4: Formulas de derivacion y de diferenciacion

Las formulas de derivacion son metodos para obtener la derivada de una funcion, segun sea su estructura sera la formula que se utilizara

Derivadas de funciones simples

Derivadas tipo potencial

Derivadas de funciones compuestas

Derivadas de tipo exponencial y logaritmicas

Referencia bibliografica

http://www.vadenumeros.es/primero/derivada-potencial-logaritmica.htm

Unidad 4: Regla de la cadena

Regla de la cadena

Regla de la cadena En las reglas básicas de derivación se aplican fórmulas apropiadas para calcular las derivadas de las funciones f C g (suma), f g (diferencia), fg (producto) y f g (cociente).

Pero no se presentó en esa sección una regla que nos diga cómo calcular la derivada de una composición de funciones; esto es, no sabemos cómo calcular la derivada de f ı g (g compuesta con f o bien g seguida de f ).

La regla de la cadena es la fórmula resultante de la derivada de la composición de funciones.

Ejemplos

Referencia bibliografica
http://canek.uam.mx/Calculo1/Teoria/Reglas/FTDelaCadena.pdf
http://www.dervor.com/derivadas/regla_cadena.html
Video : Julioprofe

Unidad 4: Propiedades de la derivada

Referencia bibliográfica

http://acreditacion.itmazatlan.edu.mx/derivada-algebraicas

Unidad 4: Concepto de diferencia interpretacion geometrica de los diferenciales

Concepto de diferencial

Diferencial Sea y = f(x) una función con su primera derivada contínua y ∆x un incremento en la variable x.
La diferencial de y se denota por dy y se define como: dy = f 0 (x) · ∆x En palabras, la diferencial de y es igual al producto de la derivada de la función multiplicada por el incremento en x

Calcula la diferencial para la función: y = x 2 + x + 1/ x

Por definición,

dy = f 0 (x) · ∆x
• Primero calculamos

f 0 (x): f 0 (x) = dy dx = 2 x + 1 − 1 x 2

• Ahora podemos calcular la diferencial multiplicando
f 0 (x) por ∆x: dy = 2 x + 1 − 1 x 2 · ∆x = 2 x∆x + ∆x − ∆x x 2

Recuerda que ∆x representa una cantidad.

No es el producto de dos cantidades: ∆ por x. Es decir, ∆x es un solo símbolo. Puedes encerrarlo entre paréntesis para evitar confusión si así lo deseas

Interpretación geométrica

Ya sabemos que la derivada de una función es la mejor aproximación lineal a la función en un punto. En particular, la derivada evaluada en un punto de la función es igual a la pendiente de la recta tangente a la función en ese punto.

En realidad estamos calculando una aproximación a ∆y (el incremento de y), suponiendo que la función es lineal en el intervalo (x0, x0 + ∆x).

Referencias bibliográficas

http://www.aprendematematicas.org.mx/notas/calcintegral/DGB6_1_1.pdf
prepa8.unam.mx

Unidad 4: Interpretación geométrica de la derivada

Se representa la posición de las distintas rectas AP (recta que une los puntos de abscisa a y a+h en la función f(x)) cuando el incremento de la variable h tiende a 0.

Interpretación geométrica de la derivada
Observamos que a medida que h se hace mas pequeño los puntos P₁,P₂,P₃,P₄ .. se aproximan al punto A y las rectas secantes AP₁,AP₂,AP₃,AP₄... tienden a la recta tangente. Las rectas AP₁,AP₂,AP₃, AP₄ que pasan por el punto A quedan determinadas por su pendiente. Esa pendiente es la tasa de variación media.

Por tanto, la pendiente de la recta tangente a la función f(x) en el punto A es:

m = lim⁡ h→0 f ( a + h) - f (a) h = f ' (a)
La pendiente de la recta tangente a f(x) en x = a coincide con la derivada en x = a

Como el punto A tiene de coordenadas (a, f(a)), la ecuación de la recta tangente en el punto A a la función f(x) es:

y - f(a) = f '(a) ( x - a)

Ejemplo
$y-f(a) = \frac{-1}{f'(a)} \cdot (x-a)$

Ejemplo 2

Halla la ecuación de la recta tangente a la curva en el punto

La fórmula es $y-f(2) = f'(2) \cdot (x-2)$
$\fbox{y-7 = 6 \cdot (x-2) }$

Referencia bibliográfica:
http://www.lemat.unican.es/lemat/proyecto_lemat/derivadas/nivel1/teoria/derivadas6.htm
http://matematicasies.com/Interpretacion-geometrica-de-la

domingo, 29 de noviembre de 2015

Unidad 4: Derivadas Concepto de incremento y razón de cambio

Concepto de razon de cambio

Razón de cambio (de una variable respecto a otra) es la magnitud del cambio de una variable por unidad de cambio de la otra. (También se le llama tasa de cambio.) Si las variables no tienen ninguna dependencia la tasa de cambio es cero. En general, en una relación funcional

y=f(x), la razón de cambio de la variable dependiente

y respecto a la independiente

x se calcula mediante un proceso de límite --de la razón

[f(x+t)−f(x)]/t, denominada cociente diferencial.

Concepto de incremento:[El incremento Dx de una variable x es el aumento o disminución que experimenta, desde un valor x = x₀ a otro x = x₁ de su campo de variación. Así, pues,

Derivada de una funcion

El concepto de derivada de una función matemática se halla íntimamente relacionado con la noción de límite. Así, la derivada se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.

Derivada de una función en un punto

Dada una función f (x), y considerado un punto a de su dominio, se llama derivada de la función en ese punto, denotada como f ¿ (a), al siguiente límite:

Este límite también puede expresarse de las dos formas alternativas siguientes:

Referencias bibliograficas
http://www.hiru.com/matematicas/derivada-de-una-funcion
https://sites.google.com/site/455laderivada/ejemplo-2